Blackjack with Perfect Pairs
You can play two games at once. You can play
the regular blackjack game and the Perfect Pair game at the Bodog and Bovada Casinos. If the Perfect Pair side game is too distracting for
you then you can play the
regular blackjack
game by itself if you want to.
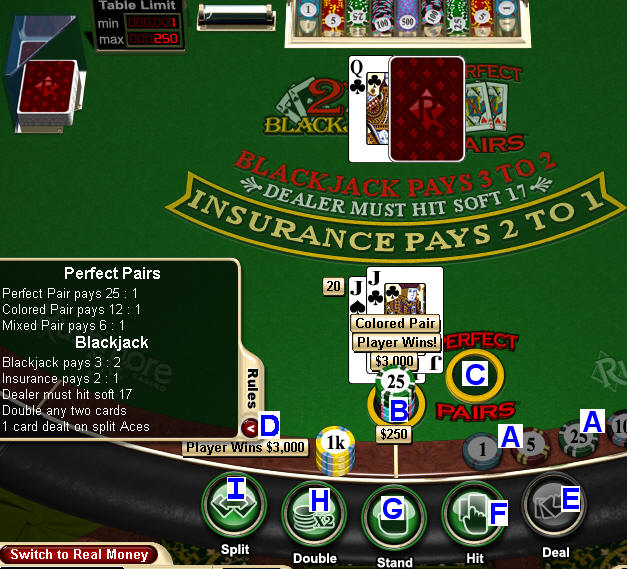
The perfect pairs game can be
played by placing a wager on the perfect pairs button. You can
wager $1 to $250 for this game. After making your wager, there
is nothing you can do to increase or decrease the amount you can
win.
Payouts are determined based on
your two initial cards. Any pair will pay out 6:1, a pair with
the same color will pay out 12:1 and two identical cards will pay
out 25:1.
Perfect Pair Pay Table
Hands |
4 Deck Probability |
8 Deck Probability |
Pay Out |
4 Deck Return* |
8 Deck Return* |
|---|---|---|---|---|---|
Perfect Pair |
1.44927% |
1.68674% |
25:1 |
$376.81 |
$438.55 |
Same Color Pair |
1.93236% |
1.92771% |
12:1 |
$251.21 |
$250.60 |
Mixed Pair |
3.86473% |
3.85542% |
6:1 |
$270.53 |
$269.88 |
Winning Hands |
7.24636% |
7.24636% |
|
$898.55 (89.9%) |
$959.03 (95.9%) |
* The expected long term return when a $1,000 is wagered.
Where to play Perfect Pairs
It is important that if you are going to be playing the
Perfect Pairs side game, that you look for a table that has at
least 8 decks of cards. Whether or not the dealer
plays through that far into the shoe is irrelevant. Just
improving your outs to available cards ratio for a Perfect Pair is good enough.
The more decks that are played, the closer the probability
is between getting a perfect pair and getting the same color
pair, which is half the pay. Between a four deck shoe
and a eight deck shoe, there is a 6% house edge difference
in favour of the eight deck shoe.
Why is it better to play with more decks in the shoe? Lets start with determining the odds of getting a perfect pair in a four deck shoe. In a four deck shoe you would need your first card to be any random card and your second card to be 3 of the remaining matching cards out of the remaining 207 cards. This works out to be a (3/207 = 1.45%) 1.45% probability or a about a one in sixty-nine chance of happening.
In a eight deck shoe you will need your first card to be any random card and your second card to be one of the seven left over matching cards out of the remaining 415 cards. There is a (7/415 = 1.69%) 1.69% chance that this will happen or a one out of every fifty-nine hands. Just in the pay out for perfect pairs you will end up winning $61.74 less at the four deck table for every $1000 that you wager.